[C’est à John von Neumann qu’est consacré le 32e article issu de Ma petite encyclopédie.
Demain l’article sera consacré à l’Ecole Estienne.
Bonne journée !]
John von Neumann
 This image comes from Los Alamos National Laboratory, a national laboratory privately operated under contract from the United States Department of Energy by Los Alamos National Security, LLC betweeen October 1, 2007 and October 31, 2018. LANL allowed anyone to use it for any purpose, provided that the copyright holder is properly attributed. Redistribution, derivative work, commercial use, and all other use is permitted. LANL requires the following text be used when crediting images to it: (link)
This image comes from Los Alamos National Laboratory, a national laboratory privately operated under contract from the United States Department of Energy by Los Alamos National Security, LLC betweeen October 1, 2007 and October 31, 2018. LANL allowed anyone to use it for any purpose, provided that the copyright holder is properly attributed. Redistribution, derivative work, commercial use, and all other use is permitted. LANL requires the following text be used when crediting images to it: (link)
Né le 28 décembre 1903 à Budapest et mort le 8 févvrier 1957 à Washington, John von Neumann est un informaticien, mathématicien et physicien hongrois qui a acquis la nationalité américaine en 1937.
Il a obtenu des résultats importants en mathématiques, en informatique, en mécanique quantique et en sciences économiques.
Enfant prodige, John von Neumann est docteur en mathématiques de l’Université de Budapest alors qu’il n’a pas encore 22 ans. Il obtient aussi un diplôme de l’Ecole polytechnique fédérale de Zurich en génie chimique.
A 25 ans il reçoit le titre de privatdozent à Berlin et à Hambourg (titre universitaire décerné aux enseignants qui ont écrit une habilitation (deuxième thèse) mais qui n’ont pas encore de poste). Titulaire d’une bourse de la fondation Rockefeller, il travaille à l’université de Göttingen avec Robert Oppenheimer sous la direction de David Hilbert. Il côtoie également Werner Heisenberg et Kurt Gödel.
En 1930, il est professeur invité à l’université de Princeton puis de 1933 à sa mort, professeur de mathématiques à l’institute for Advenced Study où il rejoint Albert Einstein et Kurt Gödel.
Naturalisé américain en 1937, il s’oriente vers les mathématiques appliquées, développe la méthode de Monte-Carlo et participe à la conception des premiers ordinateurs.
A partir de 1940 et jusqu’à sa mort il est membre du comité consultatif scientifique du Balistic Research Laboratory. De 1943 à 1955 il est consultant scientifique au laboratoire national de Los Alamos et participe au projet Manhattan (construction de de la première bombe atomique).
En 52 il devient membre du Comité consultatif général de la Commission américaine à l’énergie atomique dont il prend la direction en 1955. Il est l’un des théoriciens de la guerre froide.
Il meurt à 54 ans en 1957 d’un cancer probablement provoqué par les radiations reçues lors d’essais.
Dans le domaine informatique, John von Neumann a donné son nom à l’architecture de von Neumann qui est encore utilisée dans la quasi totalité de nos ordinateurs. Il est en particulier l’auteur de First Draft of a Report on the EDVAC dans lequel une mémoire unique contient à la fois les instructions et les données.
John vons Neumann est également à l’origine du concept d’automate cellulaire qui sera utilisé par Conway dans le jeu de la vie.
Vidéos
Excellent documentaire d’ARTE :
Bibliographie
 J. Robert Oppenheimer et John von Neumann (Source : Wikimedia Commons, domaine public)
J. Robert Oppenheimer et John von Neumann (Source : Wikimedia Commons, domaine public)
 Julian Bigelow, Herman Goldstine, Robert Oppenheimer et John von Neumann à l’Institute for Advanced Study de Princeton (Source : Wikimedia Commons, licence : Creative Commons Attribution – Partage dans les Mêmes Conditions 3.0 (non transposée)).
Julian Bigelow, Herman Goldstine, Robert Oppenheimer et John von Neumann à l’Institute for Advanced Study de Princeton (Source : Wikimedia Commons, licence : Creative Commons Attribution – Partage dans les Mêmes Conditions 3.0 (non transposée)).
 Procédé de gravure en creux utilisant une plaque de cuivre creusée par l´acide.
Procédé de gravure en creux utilisant une plaque de cuivre creusée par l´acide. Gravure réalisée en utilisant ce procédé.
Gravure réalisée en utilisant ce procédé. Jadis, acide nitrique utilisé par le procédé du même nom.
Jadis, acide nitrique utilisé par le procédé du même nom. Portrait de Georg Dorscheus, eau-forte, 1650
Portrait de Georg Dorscheus, eau-forte, 1650 Façade du théâtre de Reims en 1906
Façade du théâtre de Reims en 1906 Eau-forte datant de 1625 représentant l’église de Saint Nicaise de Reims, détruite sous la Révolution française,
Eau-forte datant de 1625 représentant l’église de Saint Nicaise de Reims, détruite sous la Révolution française, Christ Preaching (The Hundred Guilder Print)
Christ Preaching (The Hundred Guilder Print) (Source Wikimedia Commons, auteur Paul Clarke :
(Source Wikimedia Commons, auteur Paul Clarke :  (Source : Wikimedia Commons, auteur : Silvio Tanaka, licence :
(Source : Wikimedia Commons, auteur : Silvio Tanaka, licence :  Jan Łukasiewicz (Source : Wikipedia, licence : domaine public)
Jan Łukasiewicz (Source : Wikipedia, licence : domaine public) Jan Łukasiewicz, avant 1934
Jan Łukasiewicz, avant 1934 Jan Łukasiewicz, avant 1906
Jan Łukasiewicz, avant 1906 Ex-libris de Sophie Mauler (Source : Wikimedia Commons, domaine public).
Ex-libris de Sophie Mauler (Source : Wikimedia Commons, domaine public). Ex-libris de l’écrivain américain Edgar Rice Burroughs (1875-1950), dessiné par son neveu Studley Oldham Burroughs. Il représente Tarzan portant la planète mars. (Source : Wikimedia Commons, domaine public).
Ex-libris de l’écrivain américain Edgar Rice Burroughs (1875-1950), dessiné par son neveu Studley Oldham Burroughs. Il représente Tarzan portant la planète mars. (Source : Wikimedia Commons, domaine public).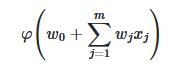
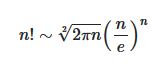

 (Fair Use)
(Fair Use) (Source Wikipedia, domaine public)
(Source Wikipedia, domaine public)